Bisect circle for a balanced set of points
is a set of points on the unit circle. No two points in lies on the same diagonal. Find a line that passes through the origin that divide the unit circle into two open semicircles, such that each piece have the same number of points in .
A harder version of this problem is Problem 1 in UIUC’s 1995 Fall Theory Qual. Let be the unit circle. The angle made by the lines and the -axis uniquely defines the line. Let the line pass through the origin with an angle be . Let , is the semicircle below the -axis, is the semicircle above the -axis. and are define the same way as .
We can solve this problem in time by reducing it to a somewhat more general problem.
Given two arcs and and a set of points on lying on the two arcs. and . for all . Find a , such that and in time.
Let’s consider an algorithm that returns line be .
Such a line must exist. Proof left as an exercise to the reader.
Note if we can solve this problem. We just need to rotate the circle so the points in the upper semicircle is at most the number of points in the lower semicircle, and then compute .
Let’s consider how to compute . First, note for any line, we can decide the number of points in the intersection of constant number of half planes in linear time. This allow us to do cardinality computations of points lying on some arc in linear time.
We can find the th point on an arc from the left by using a linear time selection algorithm.
If the lower arc contains more than points, find the th point from the left in the lower arc. Assume it intersects . We return .
So we are only dealing with the case where the lower arc contains less than points. We find the th point from the left in the lower arc. Assume it intersects , and let for a small enough epsilon(which would be apparent how small it has to be, and it can be found in linear time also.). Let . Note and , , .
- If , then we are done, return .
- If , then return .
- If , then return .
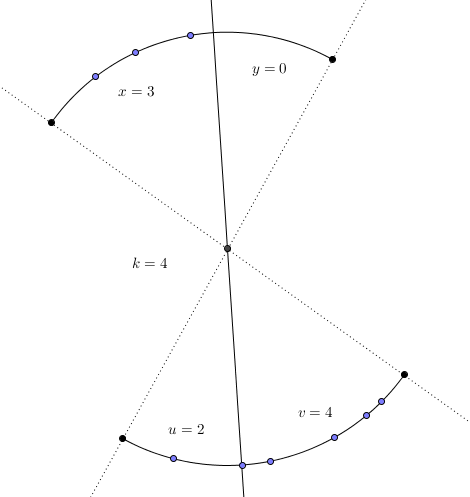
One can verify it’s valid to call the partition functions, namely the precondition for the number of points lower arc and upper arc is satisfied. There might be some off by one error somewhere. But the general idea is there.
When is small enough we solve the problem by brute force.
Every time we nest a call, we spend linear time on the current point sets, then we call the function again but with a point set of size a constant times smaller. This give us the linear time algorithm required.
This is actually a special case of the ham sandwich problem in D. There are red points and blue points on the plane. Find a line such that it divides the plane into two half-planes, so the interior of each half-plane contains at most red points and blue points. So our problem is when the red point is purely the origin.
