A generalization of the art gallery theorem with reflection and a cool problem
When I was the TA for AMS 345(Computational Geometry) last year, I have encountered problems where I don’t know if there exist a answer. Therefore I used those problem as a toy example of what a “research” could be like.
First I will demonstrate a theorem that generalize art gallery theorem. It’s the first interesting theorem I discovered. :) I’m sure someone else have found it before.
The definition of guard, visibility, etc. are defined in the wiki for the art gallery problem.
One want to generalize the notion of guarding a polygon. Instead of walls, the edges become mirrors. The light loses intensity every time it get reflected on the mirror. Therefore after reflections, it become indistinguishable to a guard.
Given polygon . . is called -reflection visible to if and only if there is a ray of light from to , such that it reflects at most times on the boundary of the polygon. Each reflection follows the law of reflection. (angle of incidence = angle of reflection.)
A -reflection guard is a guard that can see all the points that are -reflection visible from himself.
If is the minimal number of -reflection guard required to guard any polygon of vertices. Then .
By the art gallery theorem, we know . if . Since a guards can only become stronger when they can see more reflections.
The lower bound can be proved with a Chvátal’s comb with very thin teeth. A Chvátal’s comb with 3 teeth is shown below.
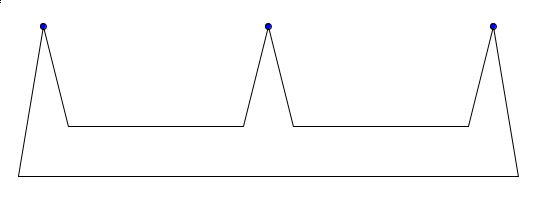
Since for each teeth, the result is symmetric. We only have to consider one teeth. Suppose we pick to be the teeth vertex. A ray can behave in 2 cases: Case 1: The ray escape the teeth after the first reflection, and bounce between the parallel lines for times. It’s easy to see the furthest distance this ray can travel from the teeth is bounded by the angle of the teeth and the distance between the lines. One can always find a polygon, such that the distance between teeth is large enough, such that no visible region from case 1 can overlap.
Case 2: The ray went into the teeth after the first reflection. One can construct a teeth such that rays will bounce inside the teeth for at least times. If is the angle of the teeth, the amount of times the ray hit the teeth is at least times. Convince yourself this is true by reflect entire teeth along it’s edge repeatedly. The ray has to hit at least all the reflections lies between a sector. One can make small enough, so . Thus all the rays in this case has to stay in the teeth, therefore it can’t overlap with visible regions of other teeth.
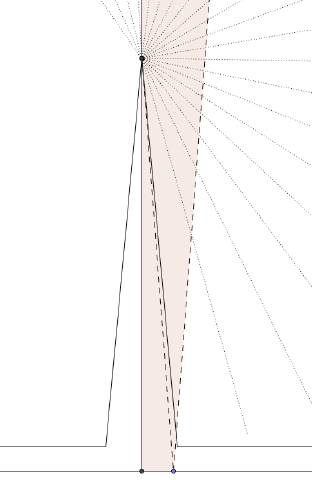
Each visible region is independent. There are visibility regions. This gives us the desired result , .
Just for fun. Here is another toy problem from last year’s AMS 345 homework.
Let be a simple polygon with vertices, for a positive integer . Starting with a vertex, color the vertices alternately around the polygon: red, blue, green, red, blue, green, etc. Find a counterexample to the following claim: There exist a monochromatic guard set.
Back then, the best known counterexample has 15 vertices(). Professor Mitchell asked if it was the smallest counterexample. I start to work on the following problem:
Find the smallest counterexample, and prove it’s the smallest.
A counterexample with . The colored region are the area can’t be seen by vertices of that color.
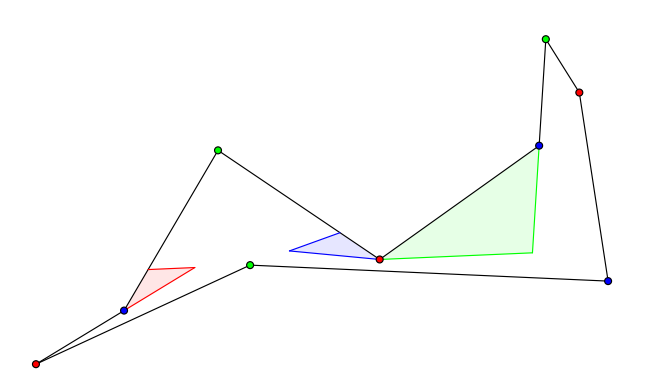
It is indeed the smallest possible.
Any 2 vertices on a quadrilateral can guard the quadrilateral.
There are only 2 cases, draw them and convince yourself.
There exist no counterexample for .
Suppose there exist a polygon such that and it is a counterexample to the original conjecture. The vertices of are .
Any triangulation of the polygon result 4 triangles. Since no color exist in all triangles(else that color guards ), there is a triangle composed of only 2 colors. Therefore one side of that triangle have the same colored end points. It must be a diagonal because no edge of have the same colored end points.
wlog, let the diagonal be . Then is partitioned to 2 quadrilaterals and . Using the lemma, we see and can guard both quadrilaterals. It implies and guards . A contradiction.
