An algorithm for covert back-to-back ticketing
Airline booking ploys are ways to circumventing airlines ticket rules in order to spend less on the ticket. We consider a special case, the back-to-back ticketing/nested ticketing. TripSavvy has a good article on back-to-back ticketing.
For many airlines, back-to-back ticketing is explicitly forbidden, this includes American Airlines, Delta and United.
We want to model back-to-back ticketing into an algorithmic problem. There is a sequence of trips between two locations, and it can be grouped into different round trips. Each round trip itinerary has a different cost. A round trip itinerary is no more than a matching between two trips.
This can be seen as simple matching problem. The vertices are trips, which we can assume a trip means “traveling from A to B on date x”. There is an edge between two trips, if there is a round trip itinerary containing the trips. The cost of the edge is the cost of buying a round trip for those two trips. Since it is also possible that we buy a one-way ticket, there are also self-loops. Also, we can consider a multigraph, where the edges are colored. Each color class represents an airline.
If one does not care about the airline finding out, it is just a minimum weight perfect matching problem allowing self-loops. However, people might actually care about airline not happy about this practice. Hence we are interested in making sure in each airline, we have no overlapping itineraries. However, we do allow overlapping itineraries across airlines.
For two edges and defined over integers, it is independent if . A set of edges is independent if the edges are pairwise independent.
Input: A multigraph where , each edge can be one of colors, and there is an edge cost function .
Output: A perfect matching (allowing self-loops), such that each color class of is independent, and the cost is minimized.
I suspect for arbitrary , the problem is NP-hard. We show how to solve the problem in polynomial time for .
Yizhi Song stated the idea that if one edge in a color is picked, it forces some edges of the other color to be picked. We can use the idea to obtain an time algorithm for this problem.
Since we are only working with case, we will let to be the color that is not . Recall and . We assume the vertices . For a graph with color classes, we define to be the subgraph consists of all edges of color . is the cost of a color edge . We define as the optimal solution when the input graph is . Intuitively, this is the optimal solution where we need to match all vertices in , but can only use colored that is fully contained in , and colored edges fully contained . We also define to be the optimal solution when the input graph is . Namely, a min-cost perfect matching covering all vertices but we can only use colored edges contained in .
The optimal solution is for either color .
We express the recursive relation. For , we have the following. It might be beneficial to see the intuition behind the two cases through the following pictures.
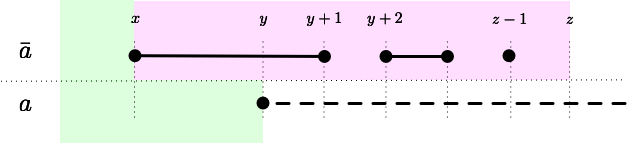
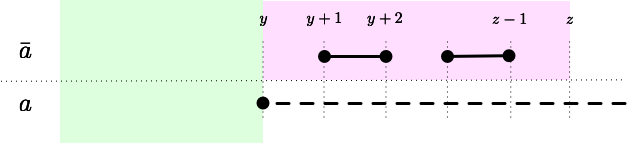
On the other hand, when One can easily infer the base case through definition. Note that all values of can be computed in time. It takes time to compute one value in . Therefore, the total running time is .
One can show that even with different airlines, there is an algorithm with running time .
